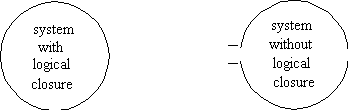The logical closure of mathematics has so
far not been possible, tough it has been looked for by a large
number of mathematicians, starting with those of the school of
logics (Leibnitz, De Morgan, Boole, Frege, Russell, Whitehead)
and continuing with those of the school of formalism (Hilbert,
von Neumann, etc.)8. The problem
of the logical closure of
mathematics is known as the problem of consistence of formal
systems. The school of formalism equals logics with mathematics.
They proved that the problem of consistence regarding the
great chapters of mathematics can be reduced to that of the consistence
of the natural numbers arithmetic, which in turn can be put
in correspondence with the set theory. But in 1931 Kurt
Goedel9 proved
the impossibility of the complete consistency of the natural numbers
arithmetic (Goedel's incompleteness theorem), thus questioning
the logical consistence of the whole mathematics, i.e. of its
logical closure. We prefer to talk of logical closure
rather than of consistence, since the normal state of the
mathematical systems is of being without logical closure (Fig.
34), which does not mean, from our point of view that they are
inconsistent. Goedel's theorem has a fundamental role in human
thinking of which we may not be yet aware: "Goedel's results
brought a mortal blow to the comprehensive axiomatization"
said Morris Kline10.
He also notes that all the results that appeared after Goedel's
work did not contribute in the least to changing the situation.
Hence, according to Morris Kline, mathematics is in a crisis since
the "efforts to follow rigorousness to its utter limits ended
up into an stalemate regarding which no common opinion has yet
be reached of what it
means"11.
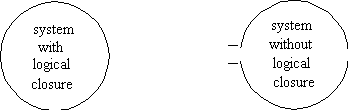
Fig. 34
I believe that things should be in principle
more clear. Accepting Goedel's result, the problems now is to
find out what it takes to "complete" the logical openness
(Fig. 35). To this purpose let's note the contributions of the
mathematical school of intuition starting with Kronecker (~1870),
continuing with Poincaré, Brower, Weyl. According to Brower,
the mathematical ideas penetrate the human mind before language,
logics and experience. The thoughts cannot be completely symbolized,
the mathematical ideas are independent of language clothing and
much richer, and logics belongs to language. According to Weyl
mathematics springs not only from the logical-rational activityof man.
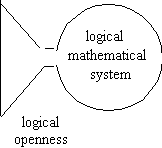
Fig. 35
The results obtained so far in the fundamental
domains of mathematics confirm Goedel's
theorem12.
An important aspect is that a formal logico-mathematical system
can be made automatic, i.e. subjected to some automated procedures
(Fig. 36).
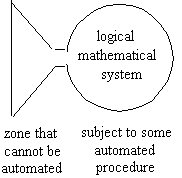
Fig. 36
Logics assumes a machine-like functioning,
the automatization of a succession of operations, and hence it
is related to the automaton within man. Cyberneticists view theproblem this
way. V. M. Gluscov13,
observing that there is no possibility
for completing a system of axioms (except some very simple cases)
stresses that " this is the important aspect of Goedel's
theorem regarding the incompleteness of arithmetics, thus throwing
on a different plane the problem of mathematical foundation and
of automatization by a complete formalization, and the process
of obtaining a new theorem through constructive-deductive
theories"14.
In a formal system there is always a part that cannot be demonstrated,
nor justified using the means of the system. Any formal system,
provided it is uncontradictory, is necessary incomplete. Since
Goedel obtained his results via logico-mathematical procedures,
his results extend to all logical systems, including the logico-mathematical
ones. If we accept the openness of such a system as a fundamental
law, then in the case of mathematics it can be open to mathematical
realities outside the logico-mathematical system, that we always
have to explore. And if everything that is logico-mathematical
can be automatized, and if the human mind has, in various
ways, the possibility to close the logic openness then
Goedel's theorem reflects a living reality of the human mind and
perhaps of the whole world.
John Lucas15
uses Goedel's theorem to conclude that the human mind, in its
totalness, cannot be explained as a machine. The only thing that
can be stated is that the human mind is not a pure logico-mathematical
machine. But nevertheless it could be a machine.
Donald MacKay16
considers the mind a stochastic automaton. Could we complete the
deterministic logico-mathematical automaton with a stochastical
one to obtain a living creature ? Our considerations so far do
not allow us to do such a thing. The way we interpret Goedel's
results is that it cannot be an automaton in itself, without openness,
whatever succession of logical systems we were to add (Fig. 37)
to complete these systems, since it always will be another openness
that we have to explore philosophically and scientifically. The
closure is not completely unknown in practice. We concretely perform
closures via the experimental results (natural sciences), via
different ways of thinking and functioning of our mind (for example
intuition). And if we go in the depth of our mind towards its
mental field and the unstructured informatter, then we ask ourselves
how deep is Goedel's openness. Partial closures are possible (Fig.
38), but a large intro-openness is always left here.
Fig. 37
Intro-Open Systems
76