Mircea Giurgiu * Results on Automatic Speech Recognition in Romanian

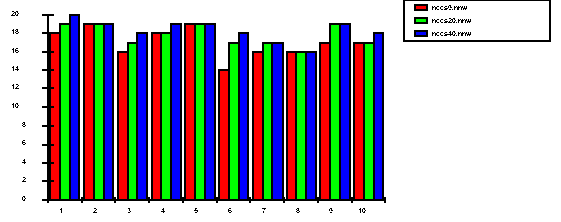
Fig. 14. - Number of recognized patterns from a total of 20 for each word with different CCSMLP.

A fixed number of segments can be applied if the duration of the utterances does not vary too much and it suits better the fixed input dimension of MLP. For each word from dictionary the segmentation error versus the number of segments has been monitored (Fig. 13), in order to find an appropriate representation for each word. When utterances are segmented into a fixed number of segments for isolated word recognition, the number of segments should be large enough to ensure sufficient temporal resolution, but, at the same time, not too large, as the time alignment effect of CCS might be lost [3].

The input of CCS algorithms is the LPC spectral representation of the words with different lengths and the minimum segment duration has been set to two. The performance (Fig. 14) of the system has been examined when varying the number of generalized centroids. It has been concluded that a number greater than 9 generalized centroids does not improve very much the recognition performance. The input in the MLP is a sequence of 9 vectors which represent the centroids of each of the segments obtained from the acoustic segmentation CCS. The inputs number in the MLP is fixed and it is 108, corresponding to a segmentation in 9 segments (the generalized centroid vector is of dimension 12 and the number of hidden units is variable: 9, 20, and 40). The influence of the number of hidden units has been evaluated in the interval 9-40: the more hidden units are, the better the recognition rate is.

Using CCS, a higher recognition rate (depending on the number of hidden units) is obtained (85%-nccs9.nnw, 89%-nccs20.nnw, 92%-nccs.nnw) as compared to MLPLPC experiment, and, at the same time, an increase in computation speed is observed.

3.3.3. Self-Organizing Feature Maps and CCS applied to Romanian speech recognition

The idea of competitive learning is as follows: assume a sequence of statistical input vectors x=x(t) from Rⁿ and a set of variable reference vectors {m_i(t),m_i from Rⁿ,i=1, 2, ..., k} that have been initialed as m_i(0) in a proper way. If x(t) is compared simultaneously with m_i(t) (t=1,2, 3, ...), then the best matching m_i(t) is updated to match even more closely the current x(t). In this way, the different reference vectors tend to become specifically "tuned" to different domains of the input variable x. Let m_c(t) be the centroid near x(t). The competitive algorithm is [11]

mc(t+1) = mc(t) + alpha(t)[x(t) - mc(t)],	if i = c		(3)
mi(t+1) = mi(t)	if i # c;

with alpha(t) a suitable monotonically decreasing function. The two essential effects leading to spatially organized maps are: (1) spatial concentration of the network activity on the cell that is best tuned to the present input, and (2) further sensitization or tuning of the best matching cell and its topological neighbors to the present input.

If we apply this theory to spoken words recognition, we must associate to each class (words) a set of centroids, in such a way that the class of the nearest neighbor for a given input vector must define the recognized object. The goal is to obtain a decision boundary among classes as good as possible. To do that, Kohonen proposes a set of strategies known as Learning Vector Quantization (LVQ). LVQ includes supervised algorithms, which need a labeled training set of data [3, 11, 12].

185