The motivation for introducing the constraint-based phonology is to have a restrictive theory of phonology that can be integrated into a general theory of language. Interactions between phonology and other levels of language can be treated uniformly. The HPSG theory [1, 2], which was developed for treating syntax and semantics, has been lately extended to phonology. Some attributes of HPSG, like lists, are treated like finite-state automata.
Unification-based formalisms were initially designed for the proper treatment of syntactic and semantic aspects of the language. The HPSG theory provides a model to store the complex information necessary in parsing. The feature structure of type sign in HPSG involves information about syntax, semantics and phonology of the object which is intended to be described. In the HPSG theory, the phonological feature of the linguistic objects was only asserted as a property, but it was not detailed. The value of the attribute PHON was the string which referenced the object described by the structure. The only operation allowed in the HPSG with the values of the attribute PHON was the concatenation.
Example:

Further work [3] extends the HPSG approach to treat phonology. The classical model for phonology is based on finite-state transducers, centered on the two-level model of Koskenniemi (1983). The new model uses finite-state automata (FSA). Because of the fact that the set of FSA forms a Boolean lattice on intersection, union and complement, the phonological descriptions can be disjoined or can be negated. New structure types can be introduced to model the phonological structure of the linguistic objects. The value of the attribute PHON will be of a new type phon, which is a nonempty list of structures. The description of this type will be given below. A structure of type list can be described as follows:
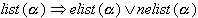
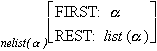
elist( * ) = [ ]
The basic operations will be the
unification and subsumption, but disjunction and negation are
also allowed.
167


