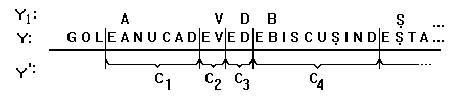Adriana Vlad, Adrian Mitrea * Estimating Conditional Probabilities and Digram Statistical Structure in Printed Romanian



By a procedure similar to that described by Shannon in [1], we extract from X a first-order Markov chain, which will represent the new information source named Y. The algorithm is suggested in Fig.1.

Λ-arbitrarily (according to case) chosen interval;
s letters - the method parameter;
ΛG - search zone for the first reoccurrence of letter G;
ΛO - search zone for the first reoccurrence of letter O;
Y - first-order Markov chain: GOL...

Fig. 1. - Extracting the first-order Markov chain for NWL.

In Fig. 1, first we have to skip over an interval consisting of Λ letters (Λ arbitrarily chosen, according to case), for avoiding certain eventual linguistic constraints from the beginning of the text and in order to assume the ergodic property for the X source. We record the letter following the Λ interval: here it is G. Then we skip over another interval consisting of s letters (s large enough, so that we can consider there is no more influence left between successive letters). After that we read until we come to the first G (ΛG interval) and record the following letter (that is O in our example). We further proceed in the same manner, that is we skip over s letters, and then letter O is searched for and we select the first letter after O (which is L, in Fig. 1). It results the sequence of letters corresponding to source Y: GOL... .

In order to have an idea about how these sequences look like we present the first 50 characters of the Y text considered in our analysis for printed Romanian: GOLEANUCADEVEDEBISCUªINDEªTADUTSADOSEROGARULADOPAR (in text without blanks).

Our method continues with the choice of a letter from the Romanian alphabet, that we shall call marker-letter, or simply marker: let it be, for example, letter E.

We now transform the texts generated by source Y into sequences of conventional words (artificial, meaningless words), all beginning with the same letter E (the marker-letter) as shown in Fig. 2:

Fig. 2. - Generating the data sample (text Y1) for the p(j/i) conditional probabilities estimation.

In this way, a new information source Y' comes out, having as symbols conventional words of Ck type (letter E appears in each conventional word only once, at the beginning).

According to Theorem 2.11 (W. Doeblin), [5], the new information source Y' is a stationary zero-memory source.

Further we obtain one more information source Y1, by recording only the letter following after the marker in the Y source texts. For example, in Fig. 2 we obtain the following sequence belonging to Y1: AVDB... .

On the basis of the above-mentioned Doeblin Theorem, it can be shown that Y1 is a stationary, zero-memory source having the same alphabet as X source, but different letter probabilities. Namely, these probabilities give exactly the information we are looking for in NWL, i.e. the conditional probabilities based on a single preceding letter which is the marker (see the Proof at the end of this section):

pY1 (j) = pY(j/E) = pX(j/E). (1)

In relation (1) the subscript letters stand for the information sources Y1, Y or X; j is an arbitrarily chosen letter from the NWL and E is the marker.

We can obviously choose any other letter i of the alphabet instead of E as marker-letter, and consequently we can determine the whole set of transition probabilities of the type pX(j/i).

In order to estimate the pX(i,j) digram probabilities in NWL we first have to determine the pX(i) letter occurrence probabilities:

pX(i,j) = pX(j/i) . pX(i). (2)

45

Previous Index Next