Adriana Vlad, Adrian Mitrea * Estimating Conditional
Probabilities and Digram Statistical Structure in Printed Romanian
Observation:
It is important to note that the proposed method led us to a stationary,
zero-memory information source Y1, which corresponds
to the i.i.d. statistical model (i.e. identically and independently
distributed random variables) assumed when estimating the probabilities
(see Section 3).
Proof of relation (1): Immediate consequence of Theorem 2.11,
[5], and of the fact that Y is the
first order Markov chain approximating to NWL.
We start with the assumption that
the procedure we have described in Fig. 1, following some Shannon's
idea, [1], leads to an ergodic first-order Markov chain, denoted
by Y; s is the method parameter value. Details on the s
parameter value do not represent the objective of this stage of
research (it will be a future presentation).
Theorem 2.11 (W. Doeblin Theorem)
states that the random variables, here consisting in the meaningless
words of type Ck, (Fig. 2), whose values are finite
order sequences of letters (states) of the Y Markov chain, all
beginning with the same state (the marker-letter) are identically
and independently distributed. That means that Y' is a
stationary, zero-memory information source.
On the basis of Doeblin Theorem
and on the fact that the functions of independent random variables
are also independent random variables, [5,6,9],
one can get another useful result. Namely, the random variables obtained when
sampling the Y Markov chain each time immediately following the occurrence
of the same state (as is marker E in Fig. 2) are independently
and identically distributed random variables (see also pp. 94,
[5]). That means that source Y1 is
a stationary, zero-memory information source, having the same alphabet as Y.
In fact source Y1 is
obtained when applying a time-invariant transformation,
[9], to
the input source Y'. Thus, each time when Y' generates
an input symbol Ck, Y1 generates a single
output letter which is either the second letter of Ck,
if Ck length is equal or larger than 2 letters, or
the marker letter, otherwise.
On the other hand, it follows
from Fig. 2 that Y1 generates letter j each
time when Y generates the same letter j on condition that
E (the marker-letter) has occurred before j. That means
that source Y1 generates j with a probability
equal to the conditional probability that j follows
E in the sequences emitted by Y: pY1(j)
= pY(j/E) .
It also follows on the account
of the procedure described in Fig. 1, that transition probabilities
of type p(j/E) are the same for the sources X and Y.
All these remarks lead directly to relation (1).
3. Estimating probabilities. Relative error determination
We attempt to estimate the p
probability of an event, on the basis of N observation
data, [6-8]. We make the assumption that these
data comply with
the i. i. d. statistical model, i. e. they come from identically
and independently distributed random variables. Denoting by m
the occurrence number of the event in the N experimental
data, the probability estimate is 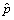 = m/N.
Considering all possible measurements of this kind (that is supposing
that the N trials are repeated many times over, and consequently
different values of m result),
= m/N.
Considering all possible measurements of this kind (that is supposing
that the N trials are repeated many times over, and consequently
different values of m result), 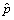 is a random variable (the respective estimator) having a binomial
distribution law, with statistical mean p, variance
p(1-p)/N, and a signal to noise ratio,
denoted by (S/N), equal to [Np/(1-p)]1/2
((S/N) represents the ratio between the statistical mean and
the standard deviation, [6]).
is a random variable (the respective estimator) having a binomial
distribution law, with statistical mean p, variance
p(1-p)/N, and a signal to noise ratio,
denoted by (S/N), equal to [Np/(1-p)]1/2
((S/N) represents the ratio between the statistical mean and
the standard deviation, [6]).
If Np(1-p) >>
1, the binomial distribution law is well approximated by the Gaussian
law (de Moivre-Laplace Theorem, [6,9]).
Expressing now the probability
that the 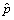 experimental value (the estimate)
differs from the p true value by a quantity not larger
than , that is P{| p -
experimental value (the estimate)
differs from the p true value by a quantity not larger
than , that is P{| p -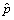 |
< &vepsilon;}=1-α,
a dependency results between N, and parameters. Concretely,
we can write:
|
< &vepsilon;}=1-α,
a dependency results between N, and parameters. Concretely,
we can write:
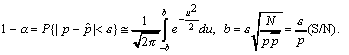 (3)
(3)
Choosing now the significance
level, or equivalently the 1-α confidence level, we can
say that in 100 (1-α)% of cases the theoretical unknown value p
will lie in an ±&vepsilon; interval around the experimental value
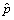 , so that:
, so that:
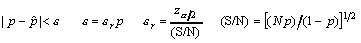 (4)
(4)
where: &vepsilon;r is
the relative error in the probability estimation;
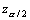 is the
α/2 - point value of the Gaussian standard distribution
(the law of mean 0 and variance 1). For instance, at 1-α
= 0.95 =>
is the
α/2 - point value of the Gaussian standard distribution
(the law of mean 0 and variance 1). For instance, at 1-α
= 0.95 => 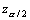 = 1.96. These are in
fact the values by which we obtained the numerical data from our illustration,
Tables 2.x - 4.x, where x=1,2.
= 1.96. These are in
fact the values by which we obtained the numerical data from our illustration,
Tables 2.x - 4.x, where x=1,2.
46



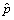 = m/N.
Considering all possible measurements of this kind (that is supposing
that the N trials are repeated many times over, and consequently
different values of m result),
= m/N.
Considering all possible measurements of this kind (that is supposing
that the N trials are repeated many times over, and consequently
different values of m result), 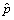 is a random variable (the respective estimator) having a binomial
distribution law, with statistical mean p, variance
p(1-p)/N, and a signal to noise ratio,
denoted by (S/N), equal to [Np/(1-p)]1/2
((S/N) represents the ratio between the statistical mean and
the standard deviation, [6]).
is a random variable (the respective estimator) having a binomial
distribution law, with statistical mean p, variance
p(1-p)/N, and a signal to noise ratio,
denoted by (S/N), equal to [Np/(1-p)]1/2
((S/N) represents the ratio between the statistical mean and
the standard deviation, [6]).
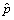 experimental value (the estimate)
differs from the p true value by a quantity not larger
than , that is P{| p -
experimental value (the estimate)
differs from the p true value by a quantity not larger
than , that is P{| p -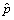 |
< &vepsilon;}=1-α,
a dependency results between N, and parameters. Concretely,
we can write:
|
< &vepsilon;}=1-α,
a dependency results between N, and parameters. Concretely,
we can write:
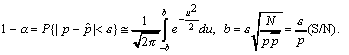
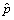 , so that:
, so that:
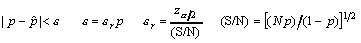
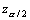 is the
α/2 - point value of the Gaussian standard distribution
(the law of mean 0 and variance 1). For instance, at 1-α
= 0.95 =>
is the
α/2 - point value of the Gaussian standard distribution
(the law of mean 0 and variance 1). For instance, at 1-α
= 0.95 => 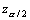 = 1.96. These are in
fact the values by which we obtained the numerical data from our illustration,
Tables 2.x - 4.x, where x=1,2.
= 1.96. These are in
fact the values by which we obtained the numerical data from our illustration,
Tables 2.x - 4.x, where x=1,2.


